准定态挂机教程:基于状态机实现
自然出怪的特点
在之前我们写的脚本中,绝大多数都假设每一波的刷新时长是一个定值。这使得脚本执行的操作与场上状态基本无关,大幅简化了脚本的编写。
但是,当我们把目光转向自然出怪长生存时,我们会面临很多新的问题:
- 两炮激活可能会刷新延迟
- 双边热过渡可能会意外刷新
- 红眼关随时可能转白
- 收尾的不确定性很大
即便是对于打法非常固定的键控炮阵,这些问题通常也是难以避免的。我们接下来逐个分析这些问题。
刷新延迟和意外刷新在实现上是可以统一的:它们通常的处理方法都是在某个时间点检查是否刷新,视结果执行不同的分支。
在转白之后,我们通常希望改用白眼/快速关的打法以节省资源。转换阵解时可能需要几个过渡波处理残留的红眼。
收尾很难有统一的应对方案,需要视所守列数和炮恢复情况而定。
状态机对前三个问题提供了一种较为泛用的解决方案。它保留了常规逐波/循环定态脚本的易写易读的优点,但同时又有一定的表达能力,足以应对自然出怪冲关的复杂条件。
状态机
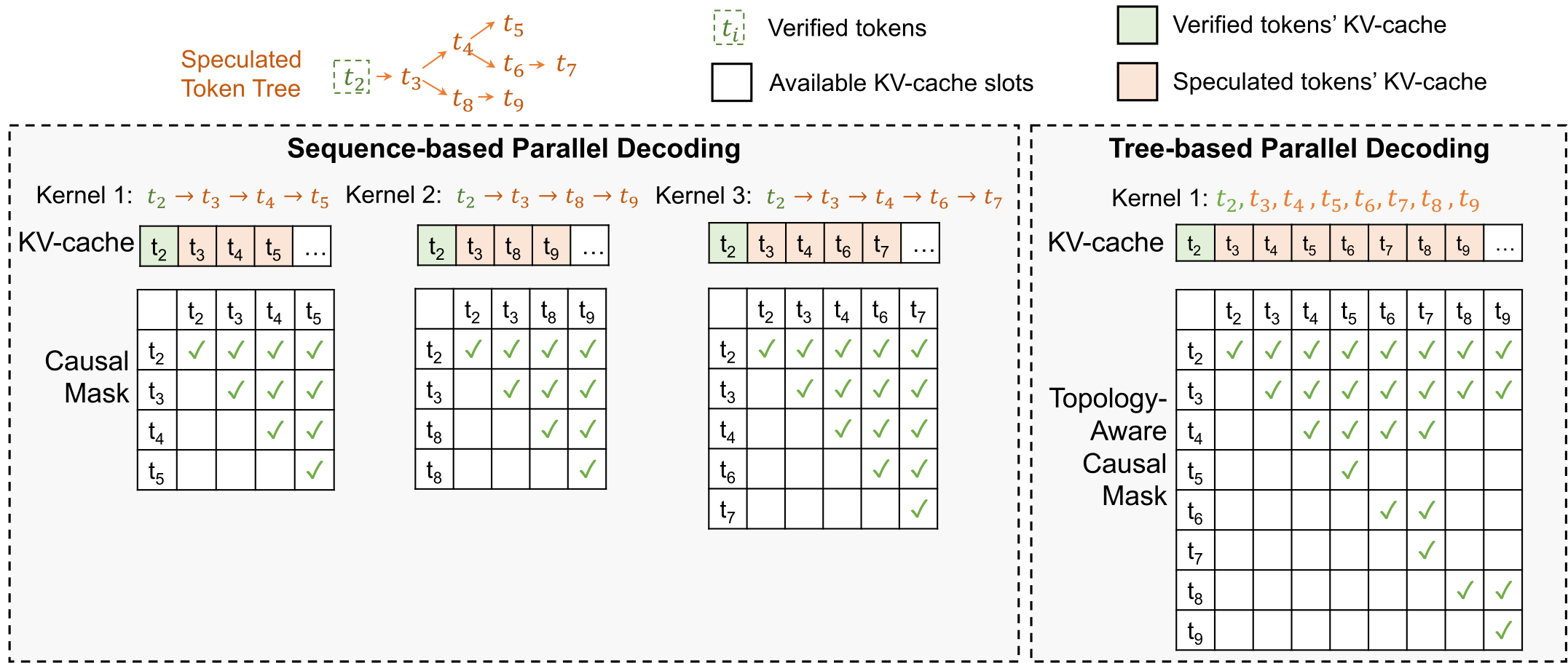
在状态机的框架下,阵解由许多个状态组成,状态之间相互连接。每个状态代表一波或其一部分。
状态之间以刷新节点为边界。什么是刷新节点呢?比如你炸了一对激活炮,这时可能激活,也可能没有激活,炮落地的瞬间就是一个刷新节点。
如果阵型里有前场自然输出,有可能你不需要做什么也会自动刷新。这种情况下,刷新节点是连续的。状态转移允许指定一个时间区间,在区间内任意时间激活视作正常激活,区间结束时仍未激活视作延迟。
在刷新节点观测到的场上信息会用来决定转移路径。如果把阵解建模成一张图,那么状态是节点,转移路径就是连接两者的有向边。比如说你执行一组操作(它们被封装在一个状态中),执行之后可能延迟,也可能激活刷新,就需要为它配置两条转移路径。如果你确信某操作不会出现刷新意外,就可以只配置一条转移路径。
每个转移路径都有触发条件。现实中,在根据刷新情况进行状态转移时,我们一般只会使用固定的几种条件。作者实现的转移函数支持以下几种条件:
- 延迟
- 激活,下波为指定波次(如w9/w19)
- 激活,下波转白
- 激活,无特殊情况
状态机的优势在于,如果脚本只使用这几种转移条件,则完全不需要自行编写判断刷新的代码,具体的判断逻辑交由预定义的转移函数处理。
本文接下来以一个经典超多炮阵型——双冰16炮为例,介绍状态机框架下代码的编写。
代码架构
状态机的核心是以下几个变量和函数:1
2
3
4
5
6
7
8
9unordered_map<string, ATimeline> states;
string lastState, currentState;
_TransitionKey activate, delay, nogiga, finish;
_TransitionKey WaveIs(std::convertible_to<int> auto... waves);
ATimeline Transition(pair<int, int> wl, auto... args);
ATimeline Transition(int wl, auto... args);
void StartTransition(int wave, const string& state);
Transition函数封装了状态转移的所有逻辑,其调用格式形如Transition(601, key1 = "next_state_name1", key2 = "next_state_name2", ...) (如果你对这种语法感到不解:在C++中,operator=可以被重载,并且返回类型可以任意指定)。其中的key可以是delay、activate、nogiga和finish,对应上一节中提到的四种转移条件(finish等效于WaveIs(9, 19))。
lastState和currentState是由Transition函数自动设置的,在运阵过程中可以读取。
states用于存储阵解,键代表状态名(可以任意取),值代表该状态对应的操作。在AScript()中,操作被逐个添加到states中,形如:1
2
3
4states["s1"] = {
Transition(601, activate = "s2", delay = "s3"),
At(300) PP(),
};
这段代码表示若当前状态为s1,则在本波300时刻发一对炮,若401时刻激活,则在下波执行状态s2;若401时刻未激活,则在本波执行状态s3。
状态机一般需要在w1和w10各启动一次(w20不需要纳入状态机中)。启动状态机的代码是:1
2StartTransition(1, "state1");
StartTransition(10, "state2");
一个完整的状态机脚本的大致结构是:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21// 状态机本身的代码
void AScript() {
// 选卡等等操作
states["s1"] = {
Transition(601, activate = "s2", delay = "s3", finish = "final1"),
// ...
};
states["s2"] = {
Transition(1200, activate = "s1", delay = "s4", finish = "final2"),
// ...
};
// ...
StartTransition(1, "s1");
StartTransition(10, "s1");
OnWave(20) {
// ...
};
}
阵解分析
主循环
本教程侧重于键控脚本编写,对阵解设计部分只是简略带过。如果对本节理解有困难可以跳过。
我们采用经典的ch6解:IPP-PP|PPDD循环。运阵过程中有两处可能发生刷新意外:
IPP刷新IPP-PP延迟
对于前一种情况,我们可以把冰波改成IPP|cPP。第二波的PP要同时全伤两波的红眼,设冰波1冰1048激活,加速波389激活(垫舞王激活的最晚时机),得出IPP波波长应为1048-389=659,对应459热过渡。加速波的红眼再冰一下,避免砸炮。
对于后一种情况,我们可以在激活炮之后再补一对炮,然后直接接下一个冰波。在执行IPP-PP|PPDD时,加速波的PP发射时本波僵尸还未刷出。本着能不读刷新倒计时就不读的态度,不妨让这对炮无论冰波是否延迟都照常发射。这样的话,冰波延迟时的激活时机为1248+291=1539。(注:由于引信延迟,实际激活时机也可能是1542。引信延迟并不会给此阵造成任何实质上的困难,但会给脚本编写增加无谓的工作量,因此脚本中关闭了引信延迟)
把状态转移关系画成图,是这样的: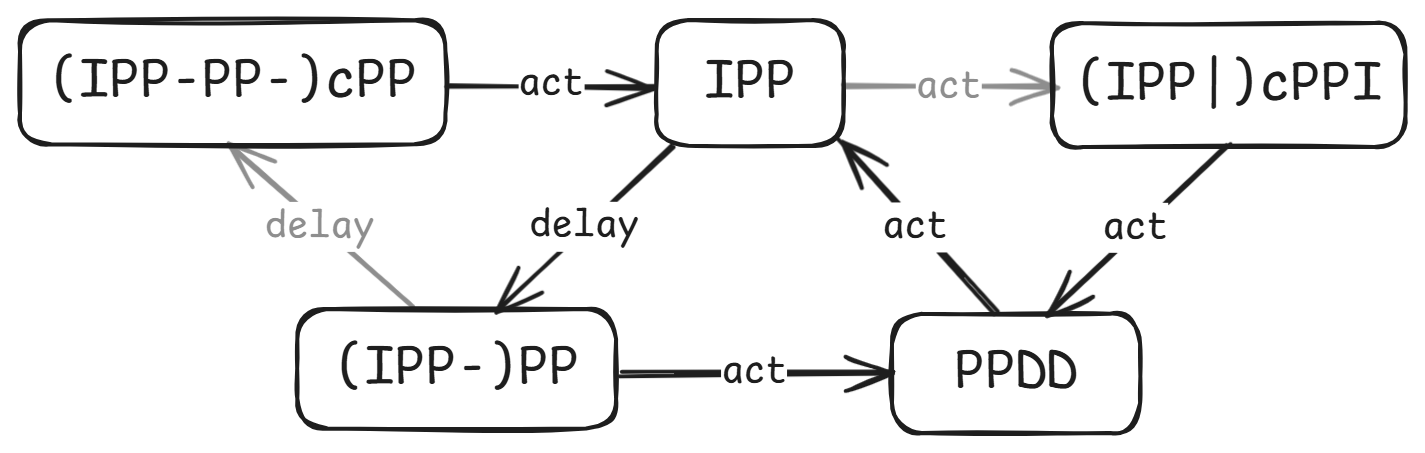
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27// 冰波:IPP-PP 1248
states["hb_IPP"] = {
Transition(659, delay = "hb_(IPP-)PP", activate = "hb_(IPP|)cPPI"),
At(1) I(),
At(459) P(15, 8.325),
At(1048) PP(8.75), // 1048 = 659 + 389
};
states["hb_(IPP-)PP"] = {
Transition(1248, activate = "hb_PPDD", delay = "hb_(IPP-PP-)cPP"),
};
// 加速波:PPDD 601
states["hb_PPDD"] = {
Transition(601, activate = "hb_IPP"),
At(291) PP() & DD<107>(9),
};
// 冰波延迟:IPP-PP-cPP 1739
states["hb_(IPP-PP-)cPP"] = {
Transition(1739, activate = "hb_IPP"),
At(1300) C.TriggerBy(AGIGA_GARGANTUAR & CURR_WAVE)(266),
At(1539) PP(), // 1539 = 1248 + 291
};
// 冰波意外刷新:IPP|cPPI 659|601
states["hb_(IPP|)cPPI"] = {
Transition(601, activate = "hb_PPDD"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
At(390) I(),
};
细心的读者可能会问:hb_(IPP|)cPPI一定不会延迟吗?事实上热过渡意外刷新和PP延迟对出怪的要求是一定程度上相互冲突的,前一波意外刷新而后一波延迟的概率极低,可以忽略。当然把这一部分补上也是不难的,具体实现就留给读者了。
首代
为了省冰,我们在w1和w10用NDD首代一波。虽然红眼关w10 PPDD不太可能延迟,但保险起见写上好了。脚本很简单,就不细讲了:1
2
3
4
5
6
7
8
9
10// 红眼关起手:NDD 601
states["hb_NDD"] = {
Transition(601, activate = "hb_PPDD", delay = "hb_(NDD-)PP"),
At(292) N({{3, 9}, {4, 9}}) & DD<106>(9),
};
// NDD延迟:NDD-PP 1092
states["hb_(NDD-)PP"] = {
Transition(1092, activate = "hb_IPP"),
At(892) PP(), // 892 = 601 + 291
};
收尾
到目前为止,我们顺利解决了w1~w8,下一个任务是w9/w19。需要注意的是,w9/w19的激活判定只考虑本波僵尸,因此可能出现w9激活后w8红眼仍在场上的情况。
收尾的处理方式需要视阵型特点而定。此阵炮数充足,收尾容错很大。ch6冰循环压力本就不大,加之此阵转白后无需用冰,不需要拖w9/w19的收尾。因此这里采用了一种比较朴素的处理方式。
首先是w9本波的激活操作。既然已经到了收尾波,没有热过渡的必要,可以直接把IPP改成PPI(由于主循环时长3700>3475,这里是能复用上的)。加速波反正早晚得冰,不如也改成PPI。唯一的例外是上波为IPP,此时本波仍需cPPI以保证全伤上波红眼。
极端条件下,可能会出现w9 401激活(对应波长1346),而场上仍有w8三血红的情况。这时虽然剩余的炮不够把它们炸死,但我们可以把这些w8红眼拖到w10。假设w9 401激活,根据w8的类型分类讨论:
IPP:剩3血红和w8撑杆,猴年马月才能砸炮。一炮收掉残余的撑杆,剩下的2血红交给w10(IPP-)PP或(IPP|)cPPI:剩2血红,1510砸炮。垫一下,交给w10收掉PPDD或(IPP-PP-)cPP:剩1血红,1161砸炮。一对炮收掉
如果w9 401没有激活,假设收尾使用8门炮,算一下可能的复用:
IPP-PP|[PP]DD|收尾|NDD|PP[DD]:收尾最短时间3475+291−601×2−398=2166,对应1221激活PPDD|I[PP]-PP|收尾|NDD|PP[DD]:收尾最短时间3475+459−1248−601−398=1687,对应742激活PPDD|IPP-[PP]-PP|收尾|NDD|PP[DD]:收尾最短时间3475+1048−1739−601−398=1785,对应840激活[PP]DD|IPP|收尾|NDD|[PP]DD:收尾最短时间3475+291−601×2−659−291=1614,对应669激活
可以看出除了第一种情况都是白给。第一种情况下,为了收掉w8的红眼,需要早于1161炸一对炮。但如果这对炮导致激活,说明w8和w9的僵尸一定都死了,不需要再炸剩下两对炮。这样复用就能宽松很多,依然不会出问题。
作为演示脚本,就不拖收尾了,直接炸掉就好。预定在1000、1500和2300发炮,如果此时已经进入w10或不存在除伴舞和小鬼之外的僵尸则取消此次发炮。
作者编写了一个简单的EndingHelper函数用于处理这种较简单的收尾。这个函数的原型是:1
2
3
4ATimeline EndingHelper(const vector<int>& times, const vector<ATimeline>& ops,
int withdrawThreshold = 0);
ATimeline EndingHelper(const vector<int>& times, const ATimeline& op,
int withdrawThreshold = 0);
它的功能是在当前波(EndingHelper执行时的波次)的times[0]时间执行ops[0],times[1]时间执行ops[1],以此类推(若ops中只有一个操作,则每次都执行ops[0])。如果场上没有僵尸(无视小鬼、伴舞,开启女仆时额外无视舞王),或者当前操作对应的时间已经超过了下一波的withdrawThreshold,则取消操作。
比如OnWave(19) EndingHelper({1200, 1800, 2400}, PP(), 0); 的含义为在w19的1200cs、1800cs和2400cs各生效一对炮,保证炮的生效时间不会在w20的0cs之后。若1200cs的炮激活了刷新,则w19的波长为2145cs,这时1800cs的炮会照常发射,但2400cs的炮会被取消。
收尾代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30states["hb_final"] = At(-200) CoDo {
// 发本波的激活炮
ATime thisWave = now + 200;
if (lastState == "hb_IPP") {
// cPPI波的处理和其他波不同
At(thisWave + 195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40);
At(thisWave + 390) I();
} else {
At(thisWave + 291) PP();
At(thisWave + 360) I();
}
co_await (thisWave + 401);
if (ANowTime(true).time < 0) {
// 如果收尾波直接刷了(波长1346)
if (lastState == "hb_IPP") {
// w8红还剩3血,w8撑杆还在;一炮收掉撑杆,红眼交给w10
At(thisWave + 900) PP();
} else if (lastState == "hb_(IPP-)PP" || lastState == "trans_cPP") {
// w8红还剩2血,1510砸炮;垫一下红眼就行
At(thisWave + 401) C.TriggerBy(AGIGA_GARGANTUAR)(800);
} else if (lastState == "hb_PPDD" || lastState == "hb_(IPP-PP-)cPP") {
// w8红还剩1血,最快1161砸炮;用炮收掉
At(thisWave + 1161) PP();
}
} else {
// 随便炸炸
At(now) EndingHelper({1000, 1500, 2300}, PP());
}
};
代码中通过读取lastState实现了对w8的分类讨论。
收尾段还有一个额外的小问题:如果w8轮到(IPP|)cPPI状态,咖啡豆CD会不够。此时需要特化处理一下这一波,去掉w8的冰,改打cPP|PPIc。为此,需要给IPP状态添加一个WaveIs(8, 18)分支:1
2
3
4
5
6
7
8
9
10
11
12
13// 冰波:IPP-PP 1248
states["hb_IPP"] = {
Transition(659, delay = "hb_(IPP-)PP", activate = "hb_(IPP|)cPPI", WaveIs(8, 18) = "hb_(IPP|)cPPI_w8", finish = "hb_final"),
At(1) I(),
At(459) P(15, 8.325),
At(1048) PP(8.75), // 1048 = 659 + 389
};
// 如果cPPI波出现在w8,需要调整为cPP|PPIc
states["hb_(IPP|)cPPI_w8"] = {
Transition(601, finish = "hb_final"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
At(next_wave + 401) C.TriggerBy(AGIGA_GARGANTUAR)(800),
};
转白
转白是大部分键控自然出怪阵型都需要考虑的事项。一方面,转白后通常可以省冰、省阳光;另一方面,转白后热过渡意外刷新的概率会明显上升。
首先考虑这个阵的白眼关阵解。打P6的话,每3波有一对多余的炮,因此可以垫两波PPDD一波,就不需要冰了。写成轨道是cPP|PPc|PPDD。
这一部分比红眼关简单得多,就不细讲了,直接上代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31states["b_PPDD"] = {
Transition(601, activate = "b_cPP", delay = "b_(PPDD)-PP", finish = "b_final"),
At(270) PP() & DD<110>(9),
};
states["b_(PPDD)-PP"] = {
Transition(1202, activate = "b_PPc", finish = "b_final"),
At(1002) PP(),
};
states["b_cPP"] = {
Transition(601, activate = "b_PPc", finish = "b_final"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
At(389) PP(8.75),
};
states["b_PPc"] = {
Transition(601, activate = "b_PPDD", finish = "b_final"),
At(318) PP(),
At(599) C.TriggerBy(APOLE_VAULTING_ZOMBIE)(1),
};
states["b_final"] = At(-200) Do {
ATime thisWave = now + 200;
if (GetCobReadyTime(4) <= 988) {
// PPDD收尾,DD于788极限全收撑杆
At(thisWave + 270) PP();
At(thisWave) EndingHelper({788}, PP());
} else {
// cPP-PP收尾
At(thisWave + 195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40);
At(thisWave + 389) PP(8.75);
At(thisWave) EndingHelper({1150}, PP());
}
};
为什么PPDD波反而要考虑延迟?因为这个状态会用在w10,而大波的普僵进场时间非常晚,401时大量铁桶、铁门仍在可伤域外,在无红关很容易造成延迟。
接下来考虑如何从红眼关阵解过渡到白眼关阵解。分类讨论最后一波红眼所在波次:
NDD、(IPP-)PP:本来也要接PPDD,直接转到白眼关阵解的PPDD即可(IPP-PP-)cPP:这波相比主循环的IPP-PP|PPDD省了一对炮,因此也能转白眼关PPDDPPDD:下一波还要处理残余2血红,不能直接转入白眼关。可以先打一波PPI作为过渡,然后转白眼关的PPcIPP:原本要接cPPI,但由于不需要压制下波红眼,可以改打cPP,然后转白眼关PPDD
插一句题外话,虽然这个解考虑了所有状态转白的情况,但如果有的状态不能转,需要接着按原阵解打下一波,状态转移函数也支持这种情况。如果nogiga分支未被指定,则接下来会继续执行activate分支,直到遇到包含nogiga分支的状态为止。
更新后的红眼关阵解如下,增加了nogiga分支和trans_PPI状态:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44// 冰波:IPP-PP 1248
states["hb_IPP"] = {
Transition(659, delay = "hb_(IPP-)PP", activate = "hb_(IPP|)cPPI", WaveIs(8, 18) = "hb_(IPP|)cPPI_w8", nogiga = "trans_cPP", finish = "hb_final"),
At(1) I(),
At(459) P(15, 8.325),
At(1048) PP(8.75), // 1048 = 659 + 389
};
states["hb_(IPP-)PP"] = {
Transition(1248, activate = "hb_PPDD", delay = "hb_(IPP-PP-)cPP", nogiga = "b_PPDD", finish = "hb_final"),
};
// 加速波:PPDD 601
states["hb_PPDD"] = {
Transition(601, activate = "hb_IPP", nogiga = "trans_PPI", finish = "hb_final"),
At(291) PP() & DD<107>(9),
};
// 冰波延迟:IPP-PP-cPP 1739
states["hb_(IPP-PP-)cPP"] = {
Transition(1739, activate = "hb_IPP", nogiga = "b_PPDD", finish = "hb_final"),
At(1300) C.TriggerBy(AGIGA_GARGANTUAR & CURR_WAVE)(266),
At(1539) PP(), // 1539 = 1248 + 291
};
// 冰波意外刷新:IPP|cPPI 659|601
states["hb_(IPP|)cPPI"] = {
Transition(601, activate = "hb_PPDD", nogiga = "b_PPDD", finish = "hb_final"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
At(390) I(),
};
// 如果cPPI波出现在w8,需要调整为cPP|PPIc
states["hb_(IPP|)cPPI_w8"] = {
Transition(601, finish = "hb_final"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
At(next_wave + 401) C.TriggerBy(AGIGA_GARGANTUAR)(800),
};
****
// 转白过渡
states["trans_PPI"] = {
Transition(601, activate = "b_PPc", finish = "b_final"),
At(318) PP(),
At(360) I(),
};
states["trans_cPP"] = {
Transition(601, activate = "b_PPDD", finish = "hb_final"),
At(195) C.TriggerBy(ADANCING_ZOMBIE, ALADDER_ZOMBIE)(40),
};
其他
现在只剩w20了!由于ch6冰平衡过于轻松,我们干脆冰消珊瑚好了:(才不是因为w19不拖的情况下w20不好打呢)1
2
3
4
5
6
7OnWave(20) {
At(96) I(),
At(380) P(15, 9), // 热过渡
At(953) PP(), // 全伤巨人
At(1220) PP(), // 全伤撑杆
EndingHelper(PP(), {1600, 2300}),
};
最后还需要启动状态机。红眼关以NDD起手,无红关以PPDD起手:1
2
3auto initialState = AGetZombieTypeList()[AGIGA_GARGANTUAR] ? "hb_NDD" : "b_PPDD";
StartTransition(1, initialState);
StartTransition(10, initialState);
附赠一个简短的天台十炮脚本,阵解主体只有23行。
总结
本文以双冰16炮键控脚本为例,展示了状态机框架的大部分核心要素。这一方法的主要优势是,使用状态机编写非定态脚本时,只需复制状态机本身的代码,并根据阵解定义新的状态和转移,无需设计复杂的嵌套或回调,也不必写大量重复的刷新检测代码。
键控炮阵冲关仍有一些难点有待解决。以下是我想到的一些,希望本文能够抛砖引玉。
其一是测试较为困难。随机发生的刷新意外和转白波次的不同都会导致轨道改变,因此执行轨迹的种类数会远多于定态演示脚本,人工分析容易有所遗漏。跳帧测试配合回放功能是一个可行的测试手段,但仍然不够高效。
其二是收尾难以系统化。可以看到,文中的阵型完全没有拖收尾。拖收尾是一件很复杂的事,上波残留僵尸、本波出红情况以及场上能垫的位置都需要考虑。笔者暂未想到能够统一大部分阵型收尾的框架。